Um pouco da História da Trigonometria
A origem da trigonometria é incerta. Entretanto, pode-se
dizer que o início do desenvolvimento da trigonometria se deu principalmente
devido aos problemas gerados pela Astronomia, Agrimensura e Navegações, por
volta do século IV ou V a.C., com os egípcios e babilônios. É possível
encontrar problemas envolvendo a cotangente no Papiro Rhind e
também uma notável tábua de secantes na tábula cuneiforme babilônica Plimpton 322.
A palavra trigonometria significa medida das partes de um triângulo. Não se sabe ao certo se o conceito da medida de ângulo surgiu com os gregos ou se eles, por contato com a civilização babilônica, adotaram suas frações sexagesimais. Mas os gregos fizeram um estudo sistemático das relações entre ângulos - ou arcos - numa circunferência e os comprimentos de suas cordas.0,
A palavra trigonometria significa medida das partes de um triângulo. Não se sabe ao certo se o conceito da medida de ângulo surgiu com os gregos ou se eles, por contato com a civilização babilônica, adotaram suas frações sexagesimais. Mas os gregos fizeram um estudo sistemático das relações entre ângulos - ou arcos - numa circunferência e os comprimentos de suas cordas.0,
O astrônomo Hiparco de
Nicéia, por volta de 180 a 125 a.C., ganhou o direito de ser chamado "o
pai da Trigonometria" pois, na segunda metade do século II a.C., fez um
tratado em doze livros em que se ocupou da construção do que deve ter sido a primeira
tabela trigonométrica, incluindo uma tábua de cordas. Evidentemente, Hiparco
fez esses cálculos para usá-los em seus estudos de Astronomia. Hiparco foi uma
figura de transição entre a astronomia babilônica e a obra de Ptolomeu. As
principais contribuições à Astronomia, atribuídas a Hiparco se constituíram na
organização de dados empíricos derivados dos babilônios, bem como na elaboração
de um catálogo estrelar, melhoramentos em constantes astronômicas importantes -
duração do mês e do ano, o tamanho da Lua, o ângulo de inclinação da eclítica -
e, finalmente, a descoberta da precessão dos equinócios.
A "Trigonometria" era então baseada no estudo da
relação entre um arco arbitrário e sua corda. Hiparco escreve a respeito do
cálculo de comprimentos das cordas. Apesar da corda de um arco não ser o seno,
uma vez conhecido o valor do seu comprimento, pode-se calcular o seno da metade
do arco, pois a metade do comprimento da corda dividido pelo comprimento do
raio do círculo é justamente esse valor, ou seja, para um círculo de raio
unitário, o comprimento da corda subtendida por um ângulo x é  conforme figura:
conforme figura:
 conforme figura:
conforme figura:
OB = r
A palavra cosseno surgiu
somente no século XVII, como sendo o seno do complemento de um ângulo. Os
conceitos de seno e cosseno foram originados
pelos problemas relativos à Astronomia, enquanto que o conceito de tangente,
ao que parece, surgiu da necessidade de calcular alturas e distâncias.
Outro matemático grego, Menelau de Alexandria,
por volta de 100 d.C., produziu um tratado sobre cordas num círculo, em seis
livros, porém vários deles se perderam. Felizmente o seu tratado Sphaerica , em três livros,
se preservou numa versão árabe e é o trabalho mais antigo conhecido sobre
trigonometria esférica.
Entretanto, a mais influente e significativa obra
trigonométrica da Antigüidade foi a Syntaxis mathematica, obra escrita
por Ptolomeu de Alexandria que contém 13 livros. Este tratado
é famoso por sua compacidade e elegância, e para distinguí-lo de outros foi
associado a ele o superlativo magiste ou "o maior". Mais tarde na
Arábia o chamaram de Almajesto, e a partir de então a obra é conhecida por esse
nome.Mostrando a mesma influência babilônica apresentada
por Hiparco,Ptolomeu dividiu a circunferência em 360 partes e o
diâmetro em 120 partes. Usou  como aproximação para o número p. Embora não fizesse uso dos termos seno e cosseno,
mas das cordas, utilizou o que pode ser considerado o prenúncio da conhecida
relação fundamental
como aproximação para o número p. Embora não fizesse uso dos termos seno e cosseno,
mas das cordas, utilizou o que pode ser considerado o prenúncio da conhecida
relação fundamental Semelhantemente,
em termos de cordas, Ptolomeu conhecia as propriedades que, em linguagem atual,
são:
Semelhantemente,
em termos de cordas, Ptolomeu conhecia as propriedades que, em linguagem atual,
são:
 como aproximação para o número p. Embora não fizesse uso dos termos seno e cosseno,
mas das cordas, utilizou o que pode ser considerado o prenúncio da conhecida
relação fundamental
como aproximação para o número p. Embora não fizesse uso dos termos seno e cosseno,
mas das cordas, utilizou o que pode ser considerado o prenúncio da conhecida
relação fundamental Semelhantemente,
em termos de cordas, Ptolomeu conhecia as propriedades que, em linguagem atual,
são:
Semelhantemente,
em termos de cordas, Ptolomeu conhecia as propriedades que, em linguagem atual,
são:
De posse do equivalente dessas fórmulas, Ptolomeu construiu
uma tabela de cordas de uma circunferência, para ângulos que variam de meio em
meio grau, entre 0º e 180º. Calculou comprimentos de cordas, inscrevendo
polígonos regulares de 3, 4, 5, 6 e 10 lados num círculo. Isso lhe possibilitou
encontrar a corda subtendida por ângulos de 36º, 60º, 72º, 90º e 120º.
Descobriu então, um método para encontrar a corda subtendida pela metade do
arco de uma corda conhecida. Esse fato que, em nossa simbologia, é o mesmo que juntamente com interpolação, permitiu-lhe calcular cordas com um bom
grau de precisão.
juntamente com interpolação, permitiu-lhe calcular cordas com um bom
grau de precisão.
Posteriormente, surgiu a necessidade de uma nova unidade de medida para
os ângulos. Foi quando surgiu o radiano, denominado radian, pois os
estudiosos discutiam uma "expressão" do ângulo em termos dep, que primeiramente foi chamada
"p-medida",
"circular" ou "medida arcual". Nenhum autor explica por que
fizeram uso dessa unidade, mas o seu uso simplificou várias fórmulas
matemáticas e físicas.
Durante seis séculos, O Almajesto, representou a mais
importante fonte de consulta para os astrônomos de todo o mundo. Porém no
século VIII é que os cientistas voltariam a sua atenção para as obras
trigonométricas de um povo, que sempre surpreendera o mundo com sua Matemática
original e criativa, os Hindus.
A mais antiga tábua de senos foi descoberta na Índia, onde essas tábuas
sem dúvida se originaram. Seus inventores, desconhecidos, conheciam as idéias
matemáticas gregas e babilônias transmitidas como subprodutos de um florescente
comércio romano com o sul da Índia, via Mar Vermelho e Oceano Índico. O Surya
Siddhanta, cujo significado é sistemas de Astronomia, era um conjunto de
textos matemáticos e regras enigmáticas de Astronomia, redigido em versos, em
sânscrito, com poucas explicações e nenhuma prova. Foi composto no século IV ou
V d.C., mas a versão que resta foi revista tantas vezes que é difícil dizer que
partes estão em sua forma original.
O primeiro aparecimento real do seno de um ângulo se deu no
trabalho dos hindus. Aryabhata, por volta do ano 500, elaborou tabelas
envolvendo metade de cordas que agora realmente são tabelas de senos e usou
jiva no lugar de seno. Esta mesma tabela foi reproduzida no trabalho
de Brahmagupta, em 628, e um método detalhado para construir uma tabela de
senos para qualquer ângulo foi dado por Bhaskaraem 1150.
Durante algum tempo os matemáticos árabes oscilaram entre o Almajesto e
a Trigonometria de jiva - de origem hindu - o conflito chegou ao final quando,
entre 850 e 929, o matemático árabe al-Battani adotou a Trigonometria
hindu, introduzindo uma preciosa inovação - o círculo de raio unitário - surgiu
o nome da função seno.
Os árabes trabalharam com senos e cossenos e, em
980, Abu'l - Wafa sabia que embora isso pudesse facilmente ter sido deduzido pela
fórmula de Ptolomeu
embora isso pudesse facilmente ter sido deduzido pela
fórmula de Ptolomeu , fazendo x = y.
, fazendo x = y.
A palavra hindu jiva - meia corda, dada ao seno foi
traduzida para o árabe que chamou o seno de jiba, uma palavra que tem o mesmo
som que jiva. Daí, jiba se tornou jaib nos
escritos árabes. A palavra árabe adequada que deveria ter sido traduzida
seria jiba, que significa a corda de um arco, em vez de jaib,
pois foi o estudo das cordas de arcos numa circunferência que originou o seno.
O nome seno vem do latim sinus que significa seio, volta,
curva, cavidade. Muitas pessoas acreditam que este nome se deve ao fato de o
gráfico da função correspondente ser bastante sinuoso. Mas, na verdade, sinus é
a tradução latina da palavra árabe jaib, que significa dobra, bolso ou prega de
uma vestimenta que não tem nada a ver com o conceito matemático de seno.
Trata-se de uma tradução defeituosa que dura até hoje. Quando os autores
europeus traduziram as palavras matemáticas árabes em latim, eles traduziram
jaib na palavra sinus. Em particular, o uso de Fibonacci do
termo sinus rectus
arcusrapidamente
encorajou o uso universal de seno.
Uma justificativa para esse erro de tradução seria o fato de que em
árabe, como em hebraico, é freqüente escrever-se apenas as consoantes das
palavras, cabendo ao leitor a colocação das vogais. Além de jibae jaib terem
as mesmas consoantes, a primeira dessas palavras era pouco comum, pois tinha
sido trazida da Índia e pertencia ao idioma sânscrito.
O termo seno certamente não foi aceito imediatamente como a notação
padrão por todos os autores em tempos, quando a notação matemática era por si
mesma uma nova idéia, muitos usaram a sua própria notação. Edmund
Gunter foi o primeiro a usar a abreviação sen em 1624 em um
desenho. O primeiro uso de sen em um livro foi em 1634 pelo matemático
francês Hérigone, enquanto Cavalieri usava Si e
Oughtred S.
Viète conhecia as fórmulas para sen nx em termos de sen x e cos x. Ele
deu explicitamente as fórmulas relativas ao seno e ao cosseno do arco triplo
As primeiras tabelas de sombras conhecidas foram produzidas pelos árabes
por volta de 860. O nome tangente foi primeiro usado por Thomas
Fincke, em 1583. O termo cotangente foi primeiro usado por Edmund
Gunter, em 1620.
As notações para a tangente e a cotangente seguiram
um desenvolvimento semelhante àquele do sen e cos.
Cavalieri usou Ta e Ta.2, Oughtred usou t
arc e co arc, enquanto Wallis usou T e t.
A abreviação comum usada hoje é tan (ou tg) sendo que a primeira ocorrência
desta abreviação é devida a Albert Girard em 1626, com tan escrito
por cima do ângulo; cot foi primeiro usada por Jonas Moore em
1674.
A secante e
a cossecante não foram usadas pelos antigos astrônomos ou
agrimensores. Estas surgiram quando os navegadores por volta do século XV começaram
a preparar tabelas. Copérnico sabia da secante que
ele chamou a hipotenusa. Viète conhecia os resultados
 juntamente com interpolação, permitiu-lhe calcular cordas com um bom
grau de precisão.
juntamente com interpolação, permitiu-lhe calcular cordas com um bom
grau de precisão.
 e
e .
.
As abreviações usadas por vários autores foram semelhantes para as
funções trigonométricas já discutidas. Cavalieri usou Se e Se.2,
Oughtred usou se arc e sec co arc, enquanto Wallis
usou s e s. Albert Girard usou sec,
escrito por cima do ângulo como ele fez para a tan. e log z
em 1702. De Moivre publicou seu famoso teorema
e log z
em 1702. De Moivre publicou seu famoso teorema
 .
.
 e log z
em 1702. De Moivre publicou seu famoso teorema
e log z
em 1702. De Moivre publicou seu famoso teorema Teoria
A trigonometria é uma ferramenta
matemática bastante utilizada no cálculo de distâncias envolvendo triângulos
retângulos. Na antiguidade, matemáticos utilizavam o conhecimento adquirido em
trigonometria para realizar cálculos ligados à astronomia, determinando a
distância, quase que precisa, entre a Terra e os demais astros do sistema
solar. Atualmente a trigonometria também é bastante utilizada e para
compreender o seu uso é necessário assimilar alguns conceitos.
Observe
a figura abaixo que representa um triângulo retângulo:
Note que o maior lado é denominado de
hipotenusa e os outros dois lados de catetos. A hipotenusa é o lado que fica
oposto ao ângulo reto (ângulo de 90o). Além do ângulo reto, há dois ângulos agudos, α
e β. A trigonometria estabelece relações entre os ângulos agudos do triângulo
retângulo e as medidas de seus lados. Vejamos quais são essas relações.
O seno de um ângulo no triângulo retângulo é a razão entre o cateto oposto e a hipotenusa.
O seno de um ângulo no triângulo retângulo é a razão entre o cateto oposto e a hipotenusa.
O cosseno de um ângulo no triângulo
retângulo é a razão entre o cateto adjacente e a hipotenusa.
A tangente de um ângulo no triângulo retângulo é a razão entre o cateto oposto e o cateto adjacente.
Definidas as razões
trigonométricas, obtemos as seguintes igualdades para o triângulo retângulo
abaixo:
Exemplo 1. Determine os valores de seno, cosseno e tangente dos
ângulos agudos do triângulo abaixo.
Solução: Temos que
Exemplo
2.
Sabendo que sen α =1/2 , determine o valor de x no triângulo retângulo abaixo:
Solução: A hipotenusa do triângulo é x
e o lado com medida conhecida é o cateto oposto ao ângulo α. Assim, temos que:
TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
O triângulo é a figura mais simples e uma das mais importantes da Geometria, ele é objeto de estudos desde os povos antigos. O triângulo possui propriedades e definições de acordo com o tamanho de seus lados e medida dos ângulos internos. Quanto aos lados, o triângulo pode ser classificado da seguinte forma:
Equilátero: possui os lados com medidas iguais.
Isósceles: possui dois lados com medidas
iguais.
Escaleno: possui todos os lados com medidas
diferentes.
Quanto aos ângulos, os triângulos podem ser
denominados:
Acutângulo: possui os ângulos internos com medidas menores que 90º
Obtusângulo: possui um dos ângulos com medida
maior que 90º.
Retângulo: possui um ângulo com medida de 90º,
chamado ângulo reto.
No triângulo retângulo existem algumas
importantes relações, uma delas é o Teorema de Pitágoras,
que diz o seguinte: “A
soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”. Essa relação é muito importante na geometria, atende inúmeras
situações envolvendo medidas.
As relações trigonométricas existentes no triângulo retângulo
admitem três casos: seno, cosseno e tangente.
Dado o triângulo retângulo ABC, temos
as seguintes relações:
Seno: cateto oposto / hipotenusa
Cosseno: cateto adjacente / hipotenusa
Tangente: cateto oposto / cateto adjacente
Tabela de Razões Trigonométricas
Os
cálculos envolvendo as relações trigonométricas, ao serem efetuados, necessitam
de alguns valores de ângulos, que estão presentes na seguinte tabela de razões
trigonométricas:
A trigonometria
possui diversas aplicações no cotidiano, abrange áreas relacionadas à
Astronomia, Física, Geometria, Navegação entre outras.
Exercícios
Resolvidos
Resolução:
Triangulo com ângulo de 60 graus
tg60 = h/d
√3 = h/d
d = h / √3 (1)
Triângulo com ângulo de 45 graus
tg45 = h/(d+10)
1 = h/(d+10)
h = d + 10 (2)
Substituindo (1) em (2):
h = h / √3 + 10 (multiplicar por √3)
h√3 = h + 10√3
h√3 – h = 10√3
h(√3 – 1) = 10√3
h = 10√3 / (√3 – 1)
Resposta: A
Questão 2 (RFB 2009 – Esaf). Um projétil é lançado com um ângulo de 30º em
relação a um plano horizontal. Considerando que a sua trajetória inicial pode
ser aproximada por uma linha reta e que sua velocidade média, nos cinco
primeiros segundos, é de 900km/h, a que altura em relação ao ponto de
lançamento este projétil estará exatamente cinco segundos após o lançamento?
a) 0,333 km
b) 0,625 km
c) 0,5 km
d) 1,3 km
e) 1 km
Resolução:
Como ele tem
velocidade média de 900 km/h, e uma hora possui 3600 segundos, temos que a
velocidade em km/seg é de 900/3600 = 0,25 km/seg. Como queremos saber a
distância após 5 segundos, ele viajou 0,25 x 5 = 1,25 km.
Observe
o triângulo que representa a trajetória do projétil. Desejamos descobrir a
altura, ou seja, o valor de x.
Temos que sen30º = cateto oposto / hipotenusa
0,5 = x / 1,25
x = 1,25 . 0,5 = 0,625 km
Resposta: B
Questão
3. (PC
MA – FGV 2012) A figura abaixo mostra uma viga AB de 4 m de comprimento
presa no ponto A a uma parede vertical. A viga é mantida na posição horizontal
pelo cabo de aço PQ de forma que P está fixo na parede, AP é vertical e Q está
no meio da viga AB. Sabe-se que o ângulo APQ mede 40º.
Dados: sen(40º) = 0,64, cos(40º) = 0,77, tg(40º) = 0,84.
A distância entre os pontos A e P é de aproximadamente:
a) 1,68 m.
b) 2,38 m.
c) 2,56 m.
d) 2,75 m.
e) 3,08 m.
Resolução
A questão informa que AB = 4. Como Q está no meio da viga AB, então AQ =
2.
Sabendo que APQ é um ângulo de 40º, vamos utilizar a fórmula da tangente
para calcularmos AP. Veja:
Resposta:
B
TRIGONOMETRIA EM UM TRIÂNGULO QUALQUER
Os problemas envolvendo
trigonometria são resolvidos através da comparação com triângulos retângulos.
Mas no cotidiano geralmente não encontramos tamanha facilidade, algumas
situações envolvem triângulos acutângulos ou triângulos obtusângulos. Nesses
casos necessitamos do auxílio da lei dos senos ou dos cossenos.
Lei dos senos
A lei dos senos estabelece relações entre as medidas dos lados com os senos dos ângulos opostos aos lados. Observe:
Exemplo 1
Aplicando a lei
dos senos, temos:
Lei dos cossenos
Nos casos em que não podemos aplicar a lei dos senos, temos o recurso da lei dos cossenos. Ela nos permite trabalhar com a medida de dois segmentos e a medida de um ângulo. Dessa forma, se dado um triângulo ABC de lados medindo a, b e c, temos:
a² = b² + c² - 2 * b * c * cos A
b² = a² + c² - 2 * a * c * cos B
c² = a² + b² - 2 * a * b * cos C
Exemplo 2
Determine o valor do lado oposto ao ângulo de 60º. Observe figura a seguir:
Nos casos em que não podemos aplicar a lei dos senos, temos o recurso da lei dos cossenos. Ela nos permite trabalhar com a medida de dois segmentos e a medida de um ângulo. Dessa forma, se dado um triângulo ABC de lados medindo a, b e c, temos:
a² = b² + c² - 2 * b * c * cos A
b² = a² + c² - 2 * a * c * cos B
c² = a² + b² - 2 * a * b * cos C
Exemplo 2
Determine o valor do lado oposto ao ângulo de 60º. Observe figura a seguir:
x² = 6² + 8² - 2
* 6 * 8 * cos 60º
x² = 36 + 64 – 96 * 1/2
x² = 100 – 48
x² = 52
√x² = √52
x = 2√13
Exemplo 3
Em um triângulo, os lados de medidas 6√3 cm e 8 cm formam um ângulo de 30º. Determine a medida do terceiro lado.
De acordo com a situação, o lado a ser determinado é oposto ao ângulo de 30º. Dessa forma, aplicamos a fórmula da lei dos cossenos da seguinte maneira:
x² = 36 + 64 – 96 * 1/2
x² = 100 – 48
x² = 52
√x² = √52
x = 2√13
Exemplo 3
Em um triângulo, os lados de medidas 6√3 cm e 8 cm formam um ângulo de 30º. Determine a medida do terceiro lado.
De acordo com a situação, o lado a ser determinado é oposto ao ângulo de 30º. Dessa forma, aplicamos a fórmula da lei dos cossenos da seguinte maneira:
x² = (6√3)² + 8² - 2 * 6√3 * 8 * cos 30º
x² = 36 * 3 + 64 – 2 * 6√3 * 8 * √3/2
x² = 108 + 64 – 96 * √3 * √3/2
x² = 172 – 48 * 3
x² = 172 – 144
x² = 28
x = 2√7 cm
Conceito
Trigonométrico
1. Arco de circunferência é
cada uma das partes em que uma circunferência fica dividida por dois de seus
pontos.
2. Medida de um arco é
realizada comparando este a um arco único, assim, para cada arco existente na
circunferência temos um ângulo central correspondente, ou seja, med(AÔB) =
med(AB). Veja o exemplo abaixo:
Os arcos unitários mais
usados são: o grau, quando dividimos a circunferência em 360 partes ele será
uma dessas 360 partes, não podemos esquecer dos submúltiplos do grau, ou seja,
o minuto 1° = 60' e o segundo 1° = 60"; e o radiano que corresponde a um
arco que tem comprimento igual ao raio da circunferência, para obter a medida
do ângulo, em radianos, basta dividir o comprimento do arco pelo raio.
Para
uma circunferência qualquer tem-se: 360° = 2π rad, logo, 180° = π rad.
Assim, usando o conceito aprendido anteriormente de proporção e conversão de
unidades temos que 1 rad ≅ 57,3°.
Circunferência
trigonométrica: os ângulos dos arcos podem ser representados por meio do ciclo
trigonométrico, para isso deve-se ter uma circunferência com raio unitário, um
plano que esteja centrado na circunferência, a origem dos arcos ser o ponto
A(1,0), os arcos medidos no sentido horário serem positivos e o dos
anti-horário serem negativos, a circunferência ficar dividida em quatro partes,
denominadas de quadrantes e numeradas no sentido anti-horário.
Não
podemos esquecer de algumas particularidades dos circunferências
trigonométricas:
→
Arcos côngruos que são arcos que quando medidos no mesmo sentido possuem a
mesma extremidade e diferem-se na quantidade de voltas. Expressão geral: α +
360º*k (caso a medida seja dado em graus) e α + 2π*k (caso a medida seja dada
em radianos), α é a menor determinação ou primeira determinação positiva sendo
0 ≤ α < 360°, ou seja, k = 0.
→
Seno de um arco: é a projeção ortogonal do segmento OM sobre o eixo y, assim,
sen α = OM".
→
Cosseno de um arco: é a projeção ortogonal do segmento OM sobre o eixo x, assim
cos α = OM'.
→
Tangente de um arco: é a medida do segmento AT, assim, tg α = AT.
Relação
fundamental da Trigonometria: sen² α + cos² α = 1.
→
Simetria dos arcos basicamente é a redução ao primeiro quadrante, assim devemos
usar formulas especificas variando da posição do arco no quadrante.
1. Arco que pertence ao 2°
quadrante: sen (180° - β) = sen β e cos (180° - β) = -cos β, logo, sen (180° -
α) = sen α e cos (180° - α) = -cos α.
2. Arco que pertence ao 3°
quadrante: sen (180° + β) = -sen β e cos (180° + β) = -cos β, logo, sen (180° +
α) = -sen α e cos (180° + α) = -cos α.
3. Arco que pertence ao 4°
quadrante: sen (360° - β) = -sen β e cos (360° - β) = cos β, logo, sen (360° -
α) = -sen α e cos (360° - α) = cos α.
Exercícios resolvidos
1. Um arco AB de uma
circunferência tem comprimento L. Se o raio da circunferência mede 4 cm, qual a
medida em radianos do arco AB, se:
(a)
L=6cm (b) L=16cm (c) L=22cm (d)
L=30cm
RESPOSTA:
A medida em radianos
de um arco AB é dada por
m(AB)=
|
comprimento do arco(AB)
comprimento do raio
|
(a) m(AB) =
( 6cm)/( 4cm) = 1,5 rad
(b) m(AB) =
(16cm)/(4cm) = 4 rad
(c) m(AB) =
(22cm)/(4cm) = 5,5 rad
(d) m(AB) =
(28cm)/(4cm) = 7 rad
2. Em uma
circunferência de raio R, calcule a medida de um arco em radianos, que tem o
triplo do comprimento do raio.
RESPOSTA:
A medida em radianos de um arco AB é
dada por
m(AB)=
|
comprimento do arco(AB)
comprimento do raio
|
Assim, como o comprimento do arco é o
triplo do comprimento do raio
m(AB) = 3R/R = 3rad
3. Um atleta percorre 1/3 de uma
pista circular, correndo sobre uma única raia. Qual é a medida do arco
percorrido em graus? E em radianos?
RESPOSTA:
Uma volta inteira na pista equivale a
360 graus, assim 1/3 de 360 graus é 120 graus.
Uma volta inteira na pista equivale a 2 radianos, então
o atleta percorreu (2/3) .
4. Em uma pista
de atletismo circular com quatro raias, a medida do raio da circunferência até
o meio da primeira raia (onde o atleta corre) é 100 metros e a distância entre
cada raia é de 2 metros. Se todos os atletas corressem até completar uma volta
inteira, quantos metros cada um dos atletas correria?
RESPOSTA:
Para simplificar os
resultados supomos pi=3,1415 e enumeramos as raias de dentro para fora como C1,
C2, C3, C4 e C5.
A primeira raia C1
tem raio de medida 10 m, então:
m(C1)=2100=200=200 x 3,1415=628,3
metros
A raia C2 tem raio de
medida 12 m, então:
m(C2)=2102=204=204 x 3,1415=640,87
metros
A raia C3 tem raio de
medida 14 m, então:
m(C3)=2104=208=208 x 3,1415=653,43
metros
A raia C4 tem raio de
medida 16 m, então:
m(C4)=2106=212=212 x 3,1415=665,99
metros
5. Qual é a
medida (em graus) de três ângulos, sendo que a soma das medidas do primeiro com
o segundo é 14 graus, a do segundo com o terceiro é 12 graus e a soma das
medidas do primeiro com o terceiro é 8 graus.
RESPOSTA: Sejam a, b e c
os três ângulos, assim
m(a)+m(b)=14
graus
m(b)+m(c)=12
graus
m(a)+m(c)= 8
graus
resolvendo o sistema
de equações, obtemos:
m(a)=5
graus
m(b)=9 graus
m(c)=3 graus
m(b)=9 graus
m(c)=3 graus
6. Qual é a medida do ângulo que o
ponteiro das horas de um relógio descreve em um minuto? Calcule o ângulo em
graus e em radianos.
RESPOSTA:
O ponteiro das horas
percorre em cada hora um ângulo de 30 graus, que corresponde a 360/12 graus.
Como 1 hora possui 60 minutos, então o ângulo percorido é igual a a=0,5 graus,
que é obtido pela regra de três:
60
min ………………… 30 graus
1 min ………………… a
graus
Convertemos agora a
medida do ângulo para radianos, para obter a=/360 rad, através da
regra de três:
180graus
………………… rad
0,5
graus ………………… a rad
7. Os dois ponteiros de um relógio
se sobrepoem à 0 horas. Em que momento os dois ponteiros coincidem pela primeira
vez novamente?
RESPOSTA:
O
ponteiro dos minutos percorre 360° enquanto o ponteiro das horas percorre
360°/12=30º. Até 1:00h os ponteiros não se encontraram, o que ocorrerá entre
1:00h e 2:00h.
Consideraremos a
situação original à 1:00h, deste instante até o momento do encontro o ponteiro
dos minutos deslocou aº e o ponteiro das horas deslocou (a-30)º, como está na
figura, assim:
Ponteiro dos minutos
|
ponteiro das horas
|
360º
|
30º
|
aº
|
(a-30)º
|
Pela tabela, tem-se
que: 360(a-30)=30.a, de onde segue que 330a=10800e assim podemos concluir que
a=32,7272º
O ponteiro dos
minutos deslocou 32,7272º após 1:00h, mas ainda precisamos verificar quantos
minutos corresponde este ângulo.
5
min ………………… 30 graus
x
min …………… 32,7272 graus
A regra de três
fornece x=5,4545'=5'27,27''. Assim, os ponteiros coincidem novamente após às
12:00h à 1 hora,5 minutos e 27,27 segundos.
8. Calcular o menor ângulo formado
pelos ponteiros de um relógio que marca 12h e 20minutos.
RESPOSTA:
O ponteiro das horas
percorre em cada hora um ângulo de 360/12 graus = 30 graus. Em vinte minutos
ele percorre o ângulo a
60
min ………… 30 graus
20
min …………… a graus
A regra de
três fornece a=10 graus, logo o ângulo formado entre os números 12 e 4 é de 120
graus, então o ângulo entre os ponteiros é 120-10=110 graus.
Parte
superior do formulário
Parte
inferior do formulário
9. Escreva o
ângulo a=12°28' em radianos.
RESPOSTA:
Usando o fato de que
1 grau possui 60 minutos, temos
1
grau …………… 60 minutos
x
graus …………… 28 minutos
A regra de três
garante que x=28/60=0,4666 grause desse modo segue que 12°
28'=(12+28/60)°=12+0,4666=12,4666°
Representando por M a
medida do ângulo em radianos, temos
180°…………… rad
12,4666°……………M
rad
e da regra de três
segue que: M=12,4666./180=0,2211 rad
10. Escreva o ângulo a=36°12'58" em radianos.
RESPOSTA:
Usando o fato de que
1 minuto possui 60 segundos, temos
1
min ……………60 segundos
x
min ……………58 segundos
x=58/60=0,967 min,
logo 36°12'58''=36°(12+0,967)'=36°12,967'
Como 1 grau
corresponde a 60', então:
1
grau ……………60 minutos
x
graus ……………12,967 minutos
x=12,967/60=0,2161° e
36°12'58''=(36+0,2161)°=36,2161°
A medida M do ângulo
em radianos, é M=36,2161°./180=0,6321 rad, que
foi obtida como solução da regra de três:
180°
…………… rad
36,2161°
……………M rad
Alunos (as): Fabiane Santos, Márcia Oliveira, Henrique
Estrela e Marta Oliveira.






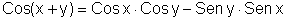








































Você está procurando um empréstimo comercial, empréstimos pessoais, empréstimos hipotecários, empréstimos para carros, empréstimos estudantis, empréstimos não consolidados para consolidação, financiamento de projetos etc ... Ou simplesmente recusar empréstimos de um banco ou instituição financeira por um ou mais motivos? Somos as soluções certas para crédito! Oferecemos empréstimos a empresas e indivíduos com taxa de juros baixa e acessível de 2%. Portanto, se você estiver interessado em um empréstimo urgente e seguro. Para mais informações, por favor envie um email hoje: Via: Elegantloanfirm@hotmail.com.
ResponderExcluir